前言:投資者們對加密資產的估值毫無疑問,都很關注,一直在探索各種估值方法。本文提到梅特卡夫定律用于對加密資產的進行估值,試圖利用梅特卡夫定律及相關變種來識別和預測價格泡沫。當然,本文的方法更多是一種探索,提供一種估值思考的方法,不一定能作為實際的投資依據。比如傳統的網絡價值是基于用戶相互交互的基礎上,比如電話、社交網絡;比特幣的活躍地址數對于整體網絡是不是有類似的價值?還不好說。大家要做好自己的判斷。本文作者Dmitry Kalichkin,由藍狐筆記社群“Kenny”翻譯。
對加密投資者來說,2018年第一季度與2017年的情況截然不同。在2017年優異的(雖然不是100%健康)60倍升值之后,加密市場經歷了劇烈調整,總網絡價值從1月1日開始的6,120億美元下降了58.2%,在第一季度末達到2560億美元。 4月份,市場出現轉機,收復了第一季度的部分價格失地。 在這些波動之后,對于當前到底是價格調整的結束還是下跌的暫時放緩的問題,許多投資者都對它感到困惑。
為了回答這個問題, CryptolabCapital使用數據驅動的方法來對加密資產估值,并研究資產價格的根本基礎。 在我們之前的文章“ 重新思考網絡價值與交易(NVT)比率”中,我們分享了一個我們使用的量化指標。 今天,很高興地告訴大家我們如何使用梅特卡夫定律對加密資產估值和進行投資決策,并介紹網絡價值與梅特卡夫比率(NVM) 。
概要
我們的目標是評估當前的比特幣價格是否由網絡活動支撐。 為此,我們使用梅特卡夫定律的不同變體,基于每日活躍地址數(Daily Active Addresses,DAA)為比特幣網絡價值構建了穩健的上限和下限。 使用這些界限,我們將比特幣網絡的自下而上的估值定義為DAA的函數。
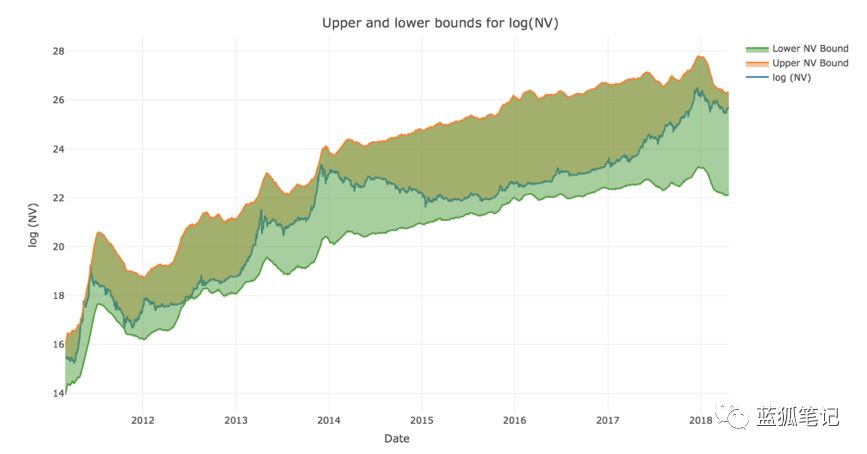
當將這個估值與不同時期的實際市場網絡價值進行比較時,我們發現歷史估值過高的情況可以通過網絡價值與梅特卡夫(NVM)比率來預測:
我們使用這個NVM比率分析了當前(截至2018年5月初)比特幣價格,并得出結論, 盡管2018年第一季度出現了重大調整,但可能還存在另一個泡沫(以及接下來的調整)。
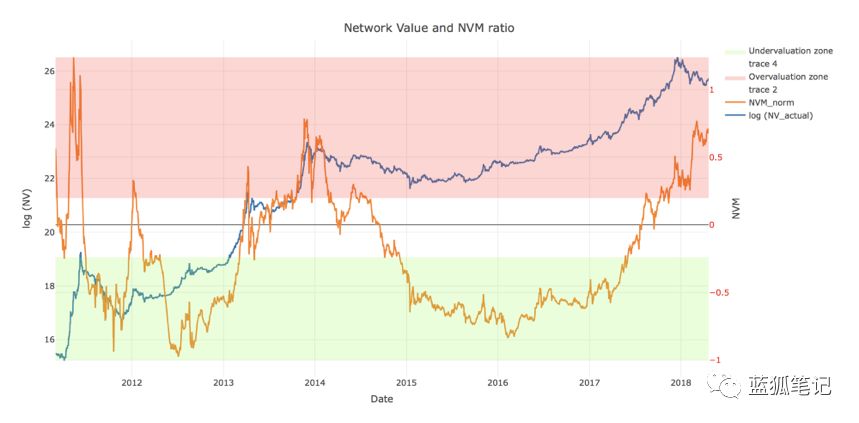
說到這一點,雖然我們看到了調整的風險,但從長遠來看,我們仍然看好比特幣的價格。
梅特卡夫定律:一切如何開始
加密資產是在數字空間中用戶連接的網絡。 用戶可以通過交換信息和參與交易來互相交互。 由于這些網絡是數字的,總是在線的,并且在區塊鏈上發布,因此網絡使用數據比其他類型的網絡(電話,傳真,即時通訊和社交媒體)更容易獲得。 交易數據可用性與公共加密市場相結合,為實時分析和評估這些網絡創造了獨特的機會。
約四十年前,施樂帕洛阿爾托研究中心(PARC)的員工羅伯特·梅特卡夫提出了網絡價值與其規模之間的關系(梅特卡夫,2013)。他表示,網絡的價值與網絡節點(用戶)的平方成正比。 這種關系基于所謂的“網絡效應”:它是經濟學和商業中描述的一種積極效果,即某種產品或服務增加了用戶,則會提升其他用戶的價值。 最初的梅特卡夫定律具有以下形式:
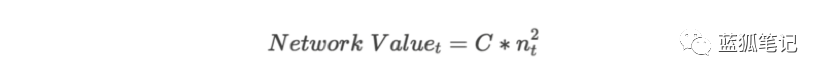
該公式背后的邏輯如下:具有n個節點的網絡中的唯一連接數可以表示為n(n-1)/2,其漸近地與n2成正比。
隨著時間的推移,這個定律的一些變體被提了出來。 例如, Andrew Odlyzko等人注意到梅特卡夫定律評估了網絡用戶之間的許多潛在聯系,而事實上,存在的局限性在于一個用戶可以擁有多少有用的連接。 他建議使用n*log n而不是n2來估算n較大情況下的網絡價值。他們同時也對原始定律有多處修改。 一些研究人員已成功應用該定律來描述Facebook和騰訊的用戶增長和財務指標。
在加密資產估值中的用法
在過去的一年中,對于利用梅特卡夫定律評估加密資產方面的主題,有著大量的研究。 CryptolabCapital對梅特卡夫定律的研究最初受到Fundstrat的Thomas Lee的啟發,他在2017年11月曾表示, 94%的比特幣價格變動可以用梅特卡夫定律來解釋 。
我們決定深入挖掘并找到Ken Alabi發表的關于這個主題的早期論文。在所有這些文章中,網絡用戶的數量通常近似于每日活躍地址 (DAA)的數量。 對于具有強大網絡效應的互聯網公司,類似的每日活躍用戶(DAU)指標是最重要的績效和估值指標之一。
Clearblocks團隊最近關于這個主題的一篇文章詳細探討了梅特卡夫定律的不同版本對比特幣價格的描述。 他們的研究揭示了3個候選的“最具預測性模型”:
原始梅特卡夫定律:NV~n2
廣義梅特卡夫定律:NV~n^1.5
Odlyzko 定律(也稱為Zipf定律):NV~n*log n
他們計算了2010年至2018年期間所有這三個定律的皮爾森相關性(Pearson correlation),并根據此分析選擇了定律2。 然后他們用它來定義價格與梅特卡夫比率,將實際網絡價值除以定律預測的值:
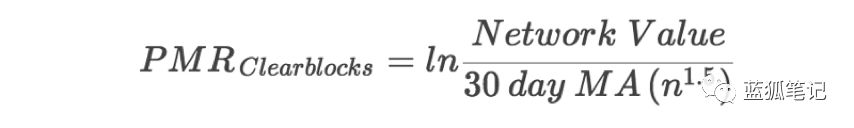
其中n是每日活躍地址(DAA),30dayMA是30天波動平均值。
然而,這里有一個問題: 很難客觀地在這三個定律之間做出選擇,Clearblocks團隊在文章中承認:
所有公式顯示與BTC的美元價格幾乎完美相關,特別是在自然對數尺度上。在任何其他領域,這種相關性將被視為巫術……這種相關性的差異非常小,可以有效地認為他們是相等的。
同時,比率的值(以及PMR分析的結果)在很大程度上取決于您為分母選擇的定律。 在預測2017年12月的泡沫和描述當前的BTC價格時,分母中的不同值會給你帶來矛盾的結果。
不同的定律——矛盾的結果
如果使用Odlyzko 定律(NV~n log n)定義PMR分母,你將得到以下公式:
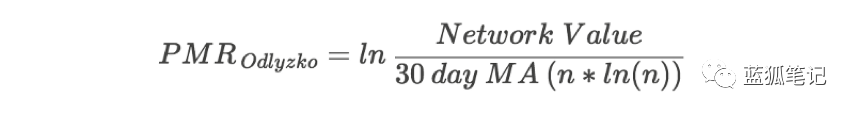
其中n是DAA。 然后根據比特幣價格繪制出Odlyzko PMR,將得到下圖。 基于這個圖表,PMR在數值等于5這個歷史最高水平,可見我們仍然處于比特幣歷史上最嚴重的泡沫中。 2018年第一季度的價格調整并沒有多大幫助——即使在2018年2月跌到約為6,000美元時,根據這個分析,比特幣仍然可能被嚴重高估。
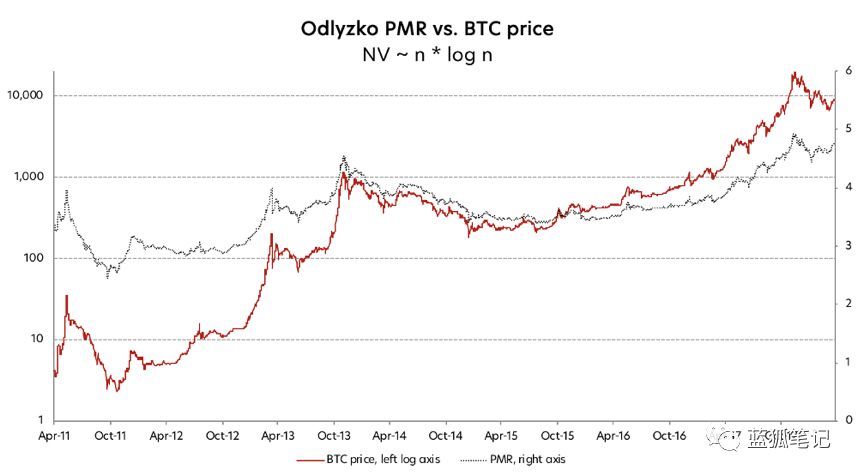
現在讓我們使用原始的梅特卡夫定律作為PMR的分母,給出以下公式:
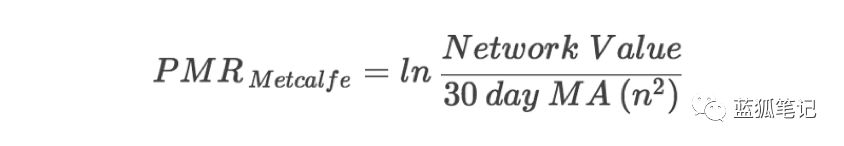
如果現在根據BTC價格繪制此PMR,你將得到非常不一樣的圖表。 仔細查看圖表,你會發現當前的PMR值約為0,這與2011年和2013年的泡沫相差無幾。而在2018年第一季度價格調整后的最低點,PMR約為-0.5。 上一次它在2014年10月和2017年8月處于同一水平。我們現在知道,這兩種情況都是購買BTC的好時機。
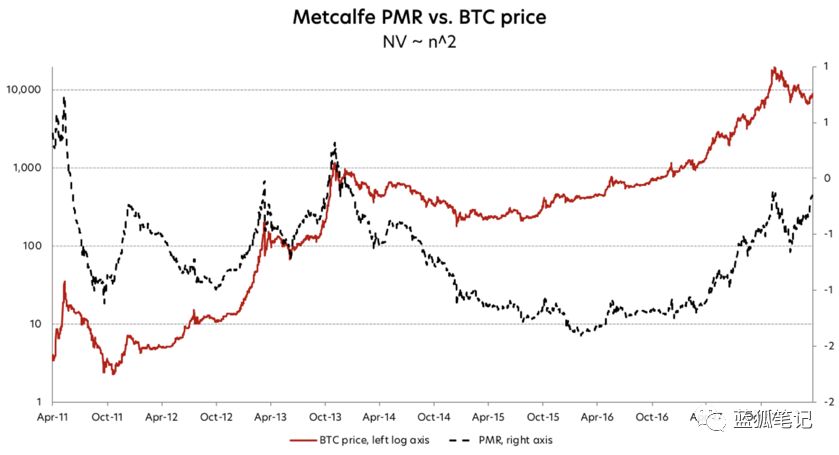
如上所述, PMR分析給出了2017年12月和2018年5月的矛盾結果,具體取決于為PMR分母選擇的定律。但,即使根據實際網絡價值與預測網絡價值之間的歷史相關性,也無法在定律之間進行選擇。
在這里我們問自己兩個問題:
我們能否為選擇最佳定律提出更好的啟發式方法?
如果不能,有沒有辦法以某種方式使用這兩個定律而不是選擇一個?
不幸的是,第一個問題的答案是“不,我們不能” 。那些對這個結論背后的代數和統計學感興趣的人可以從這里找到詳細的解釋。
幸運的是,第二個答案是肯定的。 我們使用梅特卡夫定律和Odlyzko定律來定義網絡價值的極其穩健的上限和下限,并得出一個指示比特幣被高估的比率。
兩條法則比一條法則更好
根據梅特卡夫定律背后的邏輯, n2是網絡用戶之間的一些潛在連接,實際上的局限性在于一個用戶可以擁有的有用連接數。 因此,梅特卡夫定律(NV~n2)可能高估了網絡價值,這就是為什么將其用作比特幣網絡估值的上限是合乎邏輯的。 同時我們可以使用Odlyzko定律(網絡價值~n?log n)作為下限:
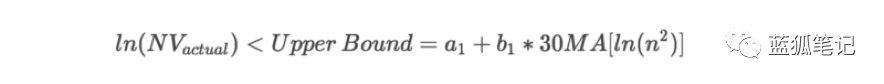
基于梅特卡夫定律的上限
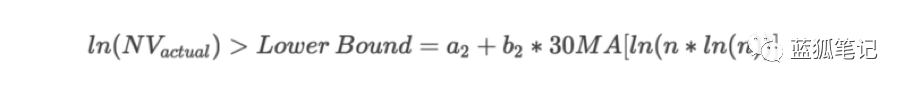
基于Odlyzko定律的下限
根據經驗選擇每個邊界的常數a和b ,以使最窄的走廊仍然覆蓋網絡值的所有波動。 為了確保我們沒有過度擬合并且未使用未來的信息,我們僅使用前2年的數據來選擇a和b。 在根據此“訓練”集修正常量之后,我們檢查了該關系是否適用于其余數據(“驗證集”)。
如果我們現在繪制網絡價值以及從梅特卡夫和Odlyzko定律得出的對應邊界圖,我們可以看到網絡價值一直穩健地保持在這些范圍內,除了2011年后的幾天之外(那時它僅僅跨越了邊界而已)。
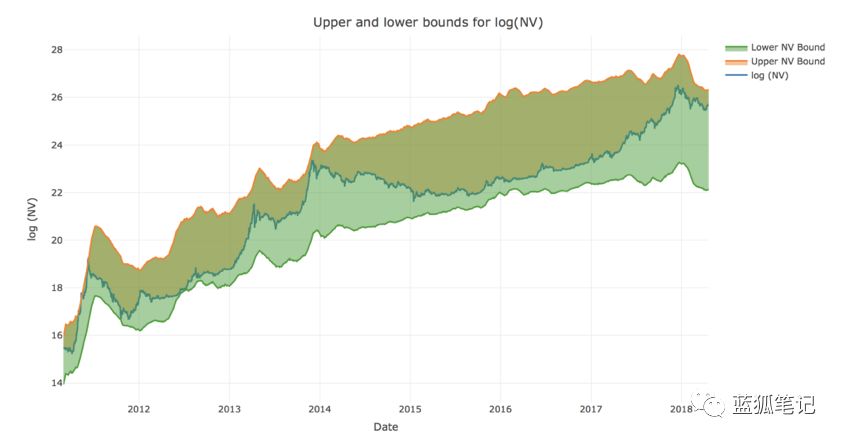
現在有了穩健的上限和下限,我們可以有信心地使用上限和下限之和的半數作為比特幣網絡自下而上的估值,得到DAA的函數:
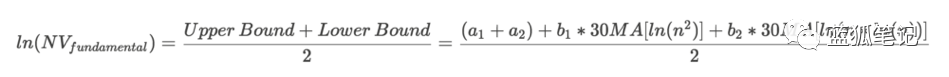
下面是實際的網絡價值和由梅特卡夫評估的基本網絡價值的圖表。 在視覺上,這種關系是驚人的。
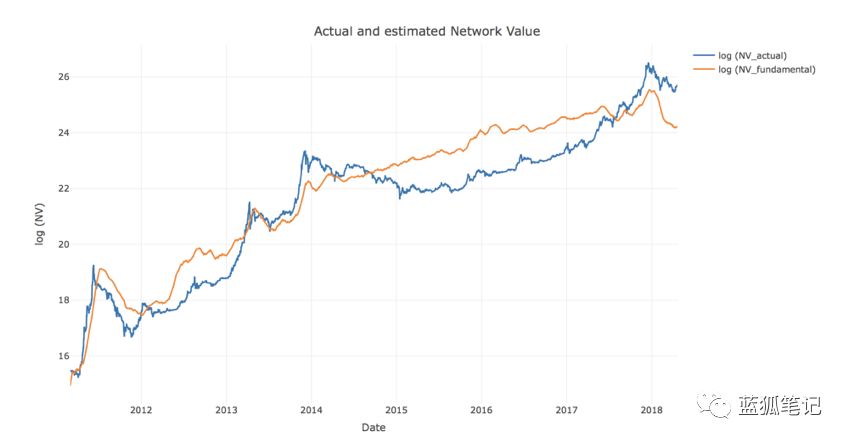
此外,在上一個帶有界限的圖表中,我們可以清楚地看到,每次網絡價值接近其上限時,接下來都會有一個調整。 相反,每當比特幣網絡價值接近下邊界時,都是投資的好時機。
使用我們新定義的梅特卡夫網絡評估法,我們可以將此邏輯形式化為一個新的、精煉的指標,我們稱之為網絡價值與梅特卡夫比率(NVM) :
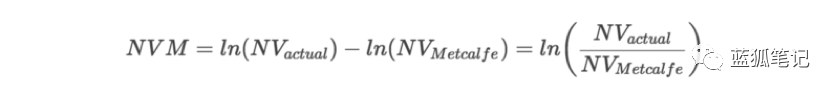
最后一個轉換:讓我們對NVM進行標準化,使其始終保持在-1和1之間,無論邊界之間的走廊有多寬:
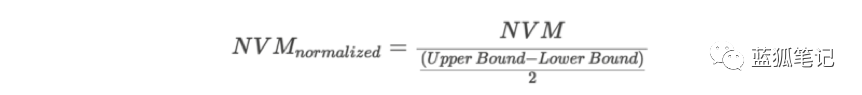
NVM描述相對于上限和下限的網絡價值位置,從而量化任何的價格高估或低估。規范化NVM為-1表示網絡值接近下限,值為1表示已達到上限。
下面是規范化NVM和比特幣網絡價值圖表。 從圖表中可以看出,高NVM已經成功預測了2011年、2012年、2013年、2014年和2017年底的調整。
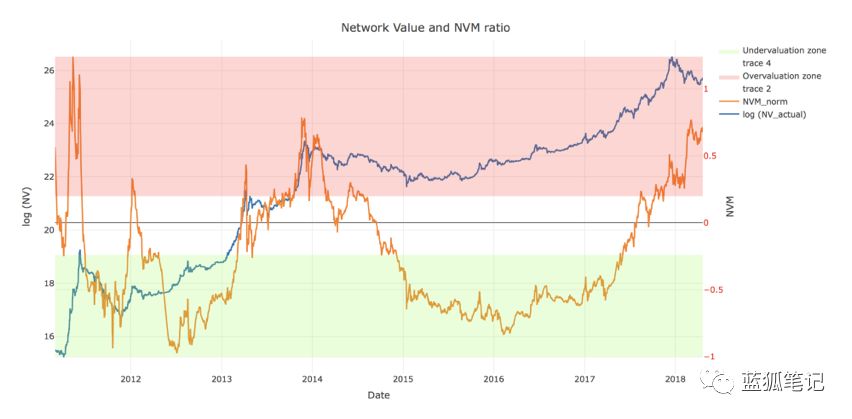
那么,我們是否處于泡沫之中?
BTC網絡值接近上限,NVM約為0.75。 目前的NVM值甚至高于2017年12月的水平,并處于2014年泡沫高峰期的水平。
與從DAA數據得出的梅特卡夫網絡價值估計相比,高NVM表明比特幣目前被高估。根據我們的模型,梅特卡夫網絡估值約為330億美元,而截至5月6日的實際網絡價值為1620億美元。 如果我們從表面上看這個結果,這意味著BTC的價值被高估了約5倍,而梅特卡夫價格約為2,000美元。 但是讓我們深入了解當前水平,并嘗試分析為什么 NVM現在處于這個水平。
讓我們來看看傳統金融中的類比。 高市盈率通常被認為是公司被高估的信號。但也可以通過商業季節性或其他因素引起的異常低的近期收益來解釋。如果當前低收益被預計為在短期內會有所增加,那么高市盈率并不一定是壞事。
讓我們嘗試將類似的邏輯應用于NVM。 基于歷史性的NVM表現,從這里可以采用以下兩種方式之一:
由于更小的分子,NVM會減少。 BTC價格調整將使網絡價值更接近(或甚至低于)梅特卡夫派生的估值。 這與我們在2014年初看到的模式類似。
由于更大的分母,NVM將減少 。 每日活躍地址增長,從而增加梅特卡夫估值并使其更接近實際網絡價值。 2012年初可以看到類似的模式。
我們來看看每日活躍地址的數量。 下圖顯示2018年第一季度的DAA顯著下降。
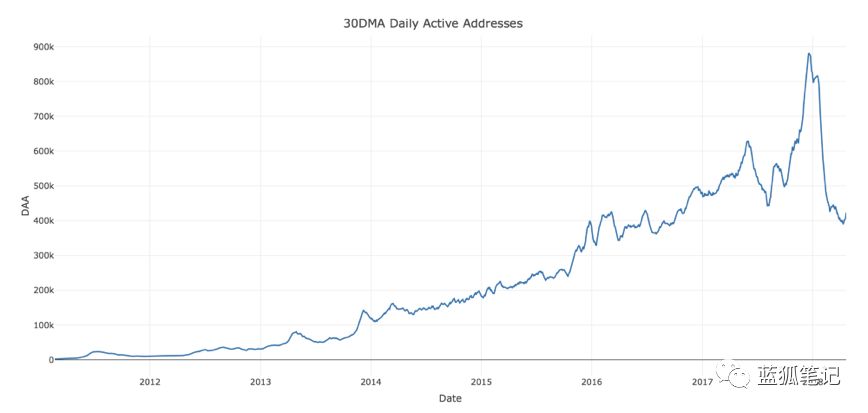
讓我們再次將2018年5月與2017年12月的情況進行比較:
總體而言,雖然目前的價格水平比2017年12月更健康,但仍未有100%基本面支撐。 投資者應密切關注相對于市場網絡價值的DAA動態。如果比特幣價格繼續增長而不會推動DAA的增長,那么可能會出現另一個泡沫(以及再一次調整)。
致謝:感謝Thomas Lee、Haseeb Quereshi , Ivan Bogatyy、Chris Burniske
、Susan Athey、ChristianCatalini、Roman Skoromnyi 的貢獻。免責聲明:本文中的任何陳述均不應視為投資建議。由于各種風險和不確定性,資產的實際表現可能與前文陳述中反映或思考的內容存在重大差異。
