前言:比特幣的共識機制是PoW,是工作量證明。在礦工中,誰有權來記賬?是通過選舉的方式?還是通過誰擁有的token更多的方式?而比特幣采用了計算謎題的方式,誰的算力大,誰就更有可能獲得解,誰就能夠獲得記賬權。而在這個算力證明的背后,是基于隨機性原理。這也是本文試圖闡述的地方,本文作者是Hugo Nguyen,來源于medium.com,由藍狐筆記公眾號“Leo”翻譯。

某種意義上控制這對骰子的規則和比特幣PoW規則類似
隨機性是構成比特幣PoW的基石。但我們是如何到這一步的?
隨機性研究簡史
隨機性一直是生活中不可或缺的一部分。很多古老的占卜儀式都是基于偶然性的:希臘人拋擲黃芪(動物指關節),中國人求簽,西非人用占卜鏈。在游戲和博彩中使用類似于骰子的設備有幾千年的歷史了。

求簽用的簽條
然而,直到16世紀,我們才開始獲得必要的工具和語言,用以理解偶然性和隨機性。這些工具包括算術概念,比如分數和零數。
我們對偶然性和隨機性的研究始于一位名為Gerolamo Cardano的人。Cardano于1501年出生于意大利,他知識淵博,是文藝復興時期最具有影響力的數學家之一。他也是出名的賭博上癮者。由于他沉迷賭博,Cardano最終陷入貧困和泯然于眾人。然而,他在賭博方面的經歷,促使他最終撰寫出一本名為“偶然性游戲的書”。(譯者注:這是市值前十的Cardano項目取名的原因嗎?用文藝復興時期數學家命名的?是巧合還是?有誰知道?)
這是第一本系統性闡述偶然性和隨機性的書籍。有意思的是,Cardano并沒有打算出版,選擇保密。在他去世很長時間,直到撰寫后的一個世紀才得以出版。

Gerolamo Cardano(1501-1576)
在理解偶然性和隨機性方面,Cardano的主要貢獻在于提出樣本空間的概念。在最基本的層面上,計算事件的概率涉及計算簡單的任務,這些任務主要是計算可能導致所述事件的場景數量。然后,將其除以所有可能場景的總數(也就是所謂“樣本空間”),同時假設所有場景可能性一致。這種假設只適用于擲骰子等問題,但這也是一個不錯的開始。
在Cardano之后,伽利略和帕斯卡也進入這個領域。伽利略是那個時代反叛知識精神的完美體現:跟強大的天主教會對立,他宣稱地球不是宇宙的中心。伽利略出版了很多重要著作。其中一本不太知名的著作是“關于骰子游戲的思考”,其中探討了Cardano所關注的類似主題。
帕斯卡跟費爾馬和笛卡爾是同時代的人,他在這個偶然性和隨機性領域比Cardano和伽利略研究更深入。他發現了所謂的“帕斯卡三角”(譯注:在中國稱為楊輝三角,中國南宋數學家楊輝在1261著述中提到該規律。)。
盡管其他文明的數學家(比如伊朗、中國和印度)比帕斯卡更早發現相同的三角形,但帕斯卡的工作最全面且增加了創新應用,特別是在概率論領域。帕斯卡還闡述了“帕斯卡的賭注”和數學期望的概念。
由于Cardano、伽利略和帕斯卡的努力,我們對偶然性和隨機性的理解逐步提升,并隨著時間的推移變得更加復雜和精致。這是文藝復興時期的一個共同主題:一些底層的突破——比如占星術、牛頓物理學、微積分、經驗主義等,這些奠定了科學的基礎,并帶來了新的知識分支以及重大的技術革新,最終導致了工業革命。
在我們剖析偶然性和隨機性的過程中,以下是值得注意的里程碑列表:
l 樣本空間
l 排列和組合
l 帕斯卡三角
l 大數定律
l 小數定律
l 貝葉斯定律——條件概率
l 鐘形曲線和標準偏差
l 回歸均值
l 隨機漫步
l 蒙特卡羅模擬
l 偽隨機性
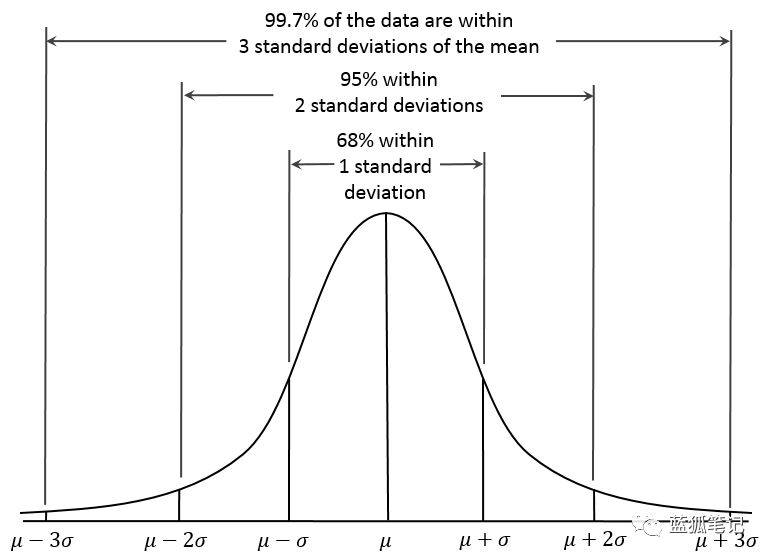
正態分布a.k.a“鐘形曲線”——圖片來自于Dan Kernler/CC 4.0
兩個主要的發展很突出:蒙特卡羅模擬和偽隨機性。特別是因為它們在當今世界中具有高度的相關性。
計算機的發明為隨機性的全新應用打開了一扇門:計算機模擬。有史以來第一次,我們有一種“預測”未來的方法,或通過廉價的實驗揭示隱藏的真相。機器提供的大量模擬在以前是不可想像的。
20世紀早期蒙特卡羅模擬的發明標志著人類歷史的一個重大轉折點。在文藝復興之前,人類經常處于對隨機性和不確定性的恐懼之中。直到20世紀,我們慢慢開始逐步提升,以更好得理解它,但仍然在很大程度上讓隨機性決定了事物的流動。通過蒙特卡羅模擬,我們開始讓隨機性為我們工作。學徒已經成為大師。
蒙特卡羅模擬的早期開拓者包括John Von Neumann和Alan Turing,兩位都是現代計算機的教父。
如今,蒙特卡羅模擬有很多應用:流體力學、商業、金融、人工智能等。最近案例有AlphaGo,它就是很好的案例,它顯示了蒙特卡羅模擬和其他技術結合后,可以給我們帶來新的發現:AlphaGo能夠用完全超出我們想象的舉動來擊敗最好的人類選手。AlphaGo挑戰了機器不可能有創造性的這一想法,并迫使我們重新思考什么是“創造力”的含義。
蒙特卡羅方法的日益普及刺激了“偽隨機性”的發展,(偽隨機過程是指過程看似是隨機的,但實際上它不是。)因為好的模擬需要能夠密切反映現實的隨機性。這個過程產生的數字是確定性的,但它們通過了被認為是“隨機”的統計測試。反過來,偽隨機性成為一個全新領域的基石之一——也是計算機時代的一個孩子——現代密碼學。
這將我們帶到了比特幣。
隨機性在比特幣中扮演的角色
比特幣的一項主要創新就是使用工作量證明來構建分布式共識。PoW提供了一個客觀的尺度,通過這個尺度,比特幣網絡的參與者可以達成共識,而無須相信網絡上的任何人。它跟PoS機制不同,PoS依賴于對共識的主觀解釋。
PoW中的W(work)涉及到尋找哈希輸出,該輸出具有最小前導零數。(哈希輸入有一些限制,例如格式化、時間戳等。)
比特幣PoW機制使用的加密哈希函數稱為SHA256。加密哈希函數的一個重要特征是它們是單向的。這意味著僅通過哈希輸出來推演哈希輸入是不可行的。它們是單向的原因很大程度上是因為哈希輸出的隨機性。
這證明是非常關鍵的,因為如果哈希功能不能產生足夠的隨機(“偽隨機”)輸出,那么,就可以從所需的輸出開始,也就是:具有特定數量的前導零的字符串,并從那里向后開始工作。這將使得“證明”最好情況下是不可靠,最壞情況下是無用。
簡單來說,典型PoW的機制所做的是(a)它提出一個問題,該問題的解存在于非常巨大的范圍內,(b)沒有捷徑,且(c)找到解的唯一方法是使用暴力計算和隨機搜索這個巨大的范圍。就像在巨大的干草堆中尋找針一樣。(計算機科學的官方術語是:“無限概率迭代程序”——相當拗口)
由此,哈希函數的隨機性決定了證明(proof)有多強。
哈希(提供)→隨機性(支持)→工作證明
“...好的謎題給予每個礦工贏得下一道謎題的機會,而機會與他們貢獻的哈希算力總量成比例。想象一下,隨機投擲飛鏢,而標靶大小跟礦工持有的算力相對應。”——Arvind Narayanan
沒有正式的證據表明,隨機性是PoW的強制性要求。但是,從經驗上看,這似乎是正確的。還有一個簡單觀察,就是說任何問題,如果它的解是非隨機的,往往需要花費努力去驗證,而首先計算解的所耗費努力也一樣多。任何這樣的機制都會導致擴展性受限制(請記住,比特幣很難擴展)。它會不成比例地偏好最快的礦工——而稍微慢一些的礦工可能一無所得。
基于隨機性的PoW的另一個好處是它在挖礦方面是開放的,任何人都可以成為礦工,來去自由。如果他們在一個區塊找到后立即加入,或者五分鐘之后加入,都沒有關系,他們獲得下一個區塊獎勵的機會不會發生變化。
哈希怎么樣?它是獲得隨機性的唯一方法嗎?可能不是。除了哈希之外,還有其他方法來模擬隨機搜索過程,例如整數分解或離散對數。
因此,哈希很可能不是實現隨機性的唯一手段,而隨機性是創建數字PoW的必要前提。
PoW方案分兩大類:
計算限制:隨機搜索受制于處理器速度
內存限制:隨機搜索受制于內存訪問
關于一個PoW類別是否真的比其他的更好還有待觀察,(我個人認為內存限制更糟糕,但潛在機制是一樣的:在一個巨大規模的范圍內,進行概率和隨機的搜索,任何解可以被廉價驗證。)
總言之,只要人類存在,我們就會因為隨機性和不確定性而掙扎。在20世紀,現代計算和蒙特卡羅模擬發明出來,這第一次使得我們可以把隨機性為我所用。在比特幣中使用隨機性標志著另外一個漫長旅途的里程碑。簡言之,工作量證明中的“證明”是由隨機性所支持的。如果沒有隨機性或者真正良好的偽隨機性,工作量證明將無效。
如果比特幣能夠成為未來的貨幣,它將代表我們迄今為止最重要和最大規模的隨機性的應用。
