黎曼猜想的證明有那么難嗎?
在這里我不列出這些證明細節,只看看一路坎坷的證明歷程:
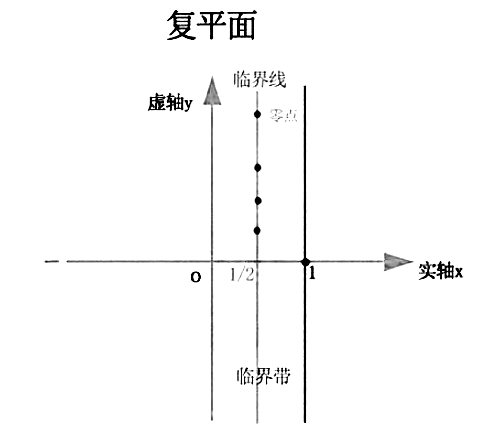
?1896年,法國的哈達瑪抵達猜想的三八臨界線邊緣——證明了黎曼ζ函數的非平凡零點只分布在帶狀區域的內部,并順手干掉了刁難人類一百年的素數定理。
?1914年,丹麥的玻爾與德國的蘭道觸到了冰山一角,窺得了黎曼ζ函數的非平凡零點傾向于“緊密團結”在臨界線的周圍。
?英國的哈代副武裝模式開啟,直接將“紅旗”插上了臨界線——證明了黎曼ζ函數有無窮多個非平凡零點位于臨界線上。
?1989年美國的康瑞又推翻了列文森的推論,重新開啟了估算的新篇章,又證明了至少有40%的零點位于臨界線上。
……
然而誰也沒能真正搞定黎曼猜想,數學上“無窮大”這只惡魔讓再多數值證據都微不足道。
沒想到,有幸之年,我竟能親身見證黎曼猜想的求證過程,實深感榮焉。
就在最近,2018年9月20日,菲爾茲和阿貝爾獎雙料得主邁克爾·阿蒂亞爵士宣稱自己求證了黎曼猜想,要在9月24日海德堡獲獎者論壇上向全世界公布證明。
一聽這消息,躲在深山老林的科學家們全炸了。
黎曼猜想這次真的會被解決嗎?作為數學獎最高得主,阿蒂亞爵士的確是這個時代頂尖數學家之一。但他都89歲了,會不會只是出來玩票……
此次阿蒂亞的證明恐與量子力學有著千絲萬縷的關系。
自20世紀以來,已有部分科學家注意到素數與量子物理之間存在聯系。
黎曼猜想中的素數行為,酷似量子力學中的“測不準原理”,雖然你可能不知道單個分子確切位置,但是你可以確定這個房間大致的分子分布,素數這難以捉摸的行為特別像量子幽靈掌握的微觀世界。
阿蒂亞若是借助量子力學這一工具來解決黎曼猜想也不是不可能。畢竟,數學中很多重大問題,都是建立在與其他數學分支跨界聯系的基礎上才被解決,比如費馬大定理。
而由量子理論所衍生而出的量子計算機,也早已被數學家證明能快速對大數進行質因數分解,基于“平行世界”的運算可輕而易舉破解素數并顛覆密碼系統。
量子力學與素數的戀情,也許將在這一次揭開情人面紗。
