摘要
Markowitz投資組合理論是金融學領域的經典理論,它奠定了現代投資理論發展的基礎,這一理論很好地回答了在既定風險水平的基礎上,如何使投資的可能預期收益率極大,或為獲得既定的預期收益率,如何使承擔的風險極小的問題,本文將通過將該理論應用到數字貨幣的交易中,測試通過投資組合分散投資對提高投資收益和分散風險的作用。
目 錄
1. 數據準備
2. 數據處理
3. 數學建模
4. 結果展示
5. 結論
報告正文
我們將基于最經典的Markowitz投資組合理論建立數學模型,結合市值前10的幣種的歷史數據對該模型分散風險的效果進行評估,并試圖說明按適當權重建立投資組合能有效地分散非系統風險。
1、 數據準備
我們以市值前10的數字貨幣從2017年11月30日到2018年5月21日在 coinmarketcap 上面每天凌晨0點的價格數據為例,用來測試Markowitz投資組合理論的風險分散效果。
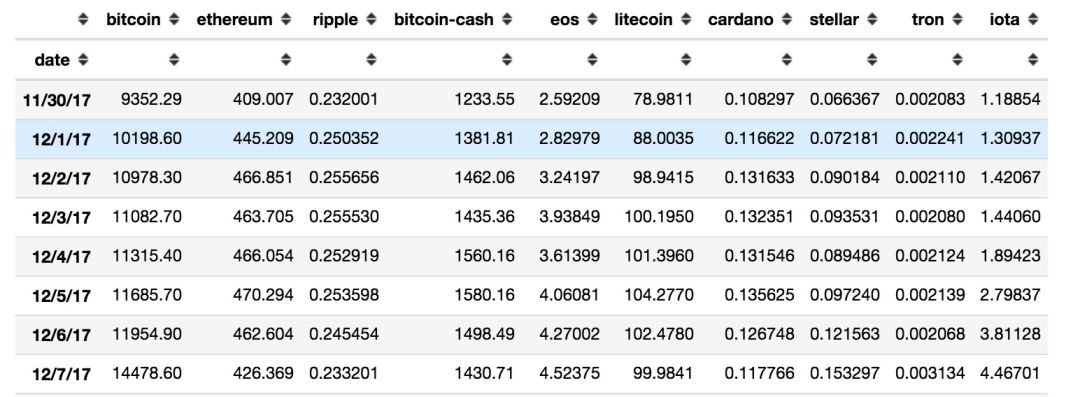
2、數據處理
將利用價格數據計算日收益率
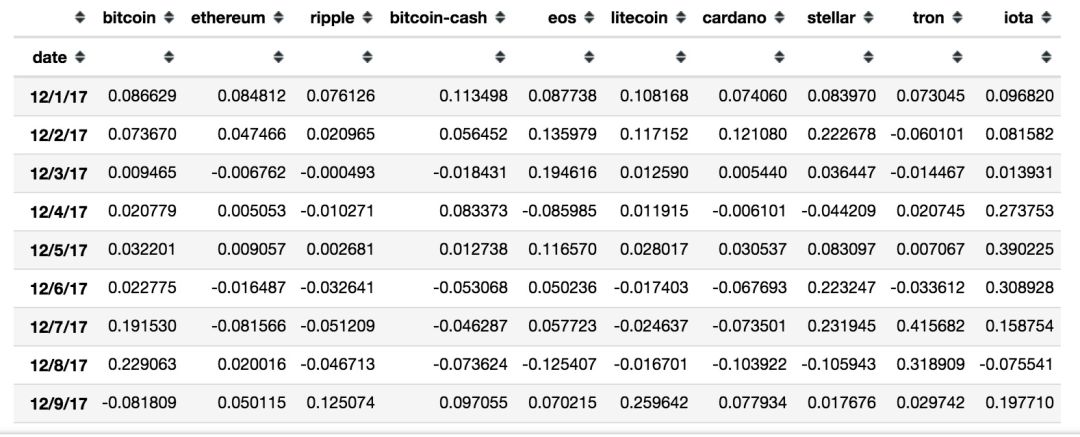
利用日收益率數據計算各幣種的方差和夏普比率
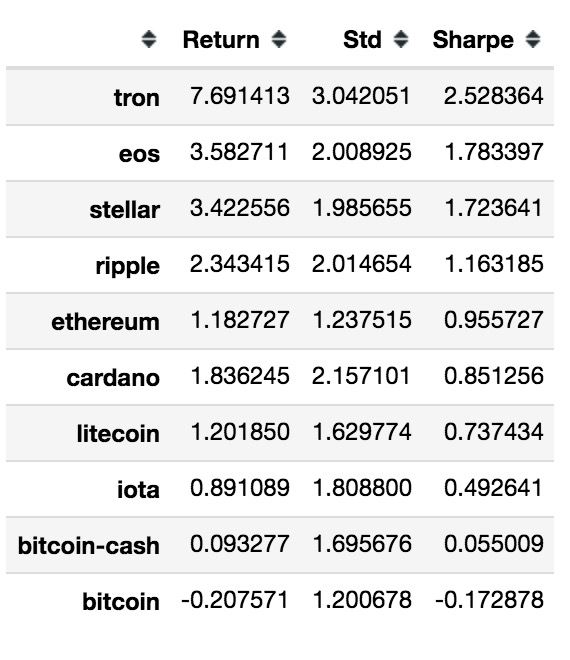
計算各幣種收益率的協方差和相關系數
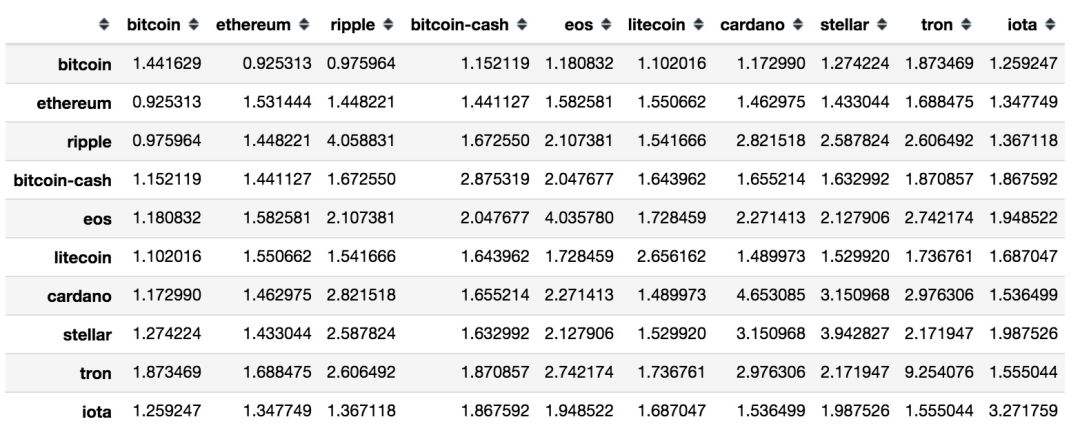
協方差矩陣
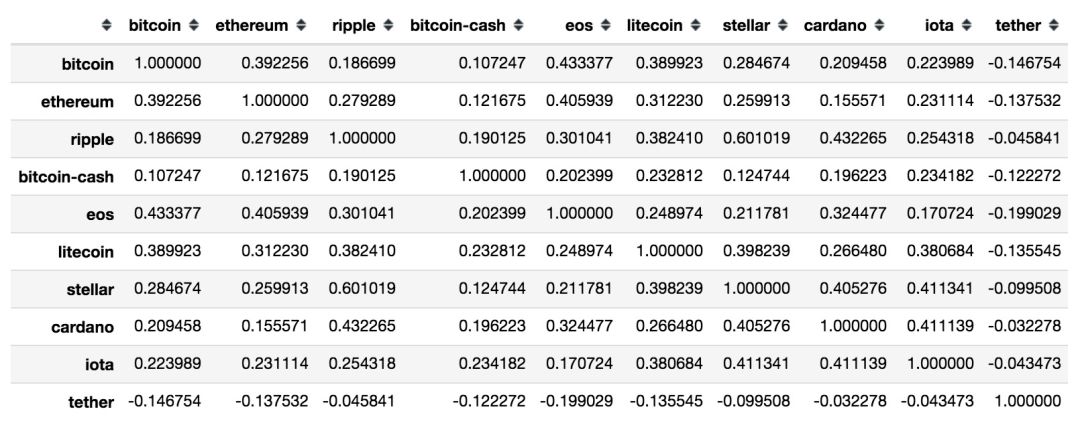
相關系數矩陣
3、 數學建模
根據Markowitz投資組合理論的基本原理,把10個幣種當做成分建立投資組合,對組合中的每一個成分賦予一定權重,總權重為1,就能夠分散風險,在固定所能承受的風險下,追求最大的報酬;或在固定的預期報酬下,追求最低的風險。在這里,我們用日收益的標準差衡量風險,用夏普比率衡量風險分散的效果,即: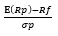 ,
,
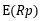 ,為投資組合的期望收益,
,為投資組合的期望收益,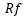 為無風險利率,為了模型的簡單,我們假定其為0,
為無風險利率,為了模型的簡單,我們假定其為0,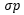 為投資組合的標準差,夏普比率的意義在于,用于衡量單位風險能獲得的收益的大小。
為投資組合的標準差,夏普比率的意義在于,用于衡量單位風險能獲得的收益的大小。
我們采用隨機模擬的方式,在①每個成分的權重都大于0,②各成分的權重和為1的約束條件下,隨機調整投資組合中各成分的權重,然后分別計算出標準差,收益和夏普比率,并繪制出散點圖。當嘗試次數足夠多的時候,就能在散點圖中看到投資組合的有效邊界和最優投資組合,在這里,我們選擇嘗試50萬次就夠了。
4、結果展示
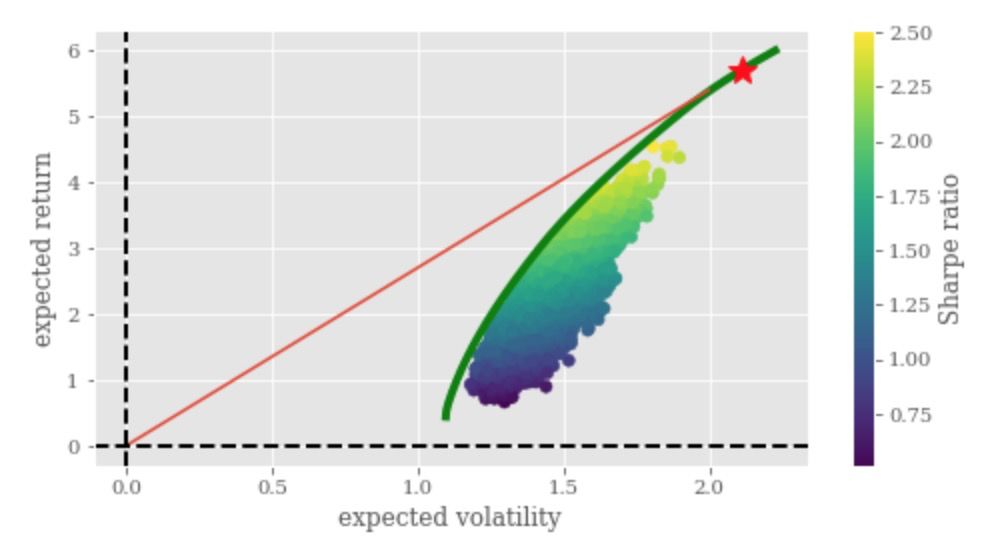
通過50萬次隨機嘗試繪制出的散點圖,橫軸代表標準差,縱軸代表期望收益,夏普比率的大小由散點顏色的深淺來表示。從圖中我們可以看到,位置越靠近下圖的左上方區域,夏普比率越大,即風險分散的效果越好。這些處于左上方的點構成了投資組合的有效邊界:也就是在給定標準差的情況下,收益率最大的投資組合的集合。
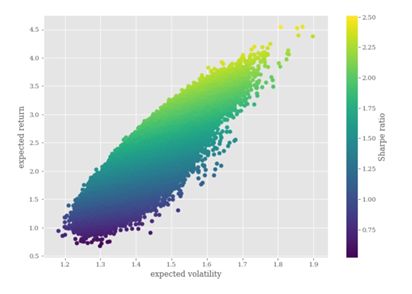
然后就可以繪制出投資組合的有效邊界,并且找出夏普比率最大的投資組合,用紅色五角星標記出來。
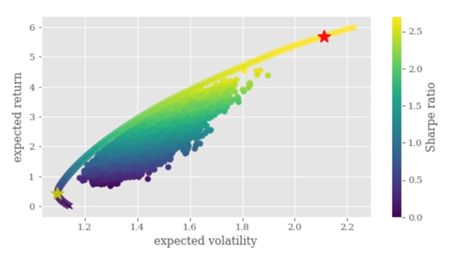
隨后就可以連接原點(因為我們假定無風險收益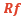 為0)和紅色五角星標記出的點,繪制出資本市場線,即沿著投資組合的有效邊界,由風險資產和無風險資產構成的投資組合。
為0)和紅色五角星標記出的點,繪制出資本市場線,即沿著投資組合的有效邊界,由風險資產和無風險資產構成的投資組合。
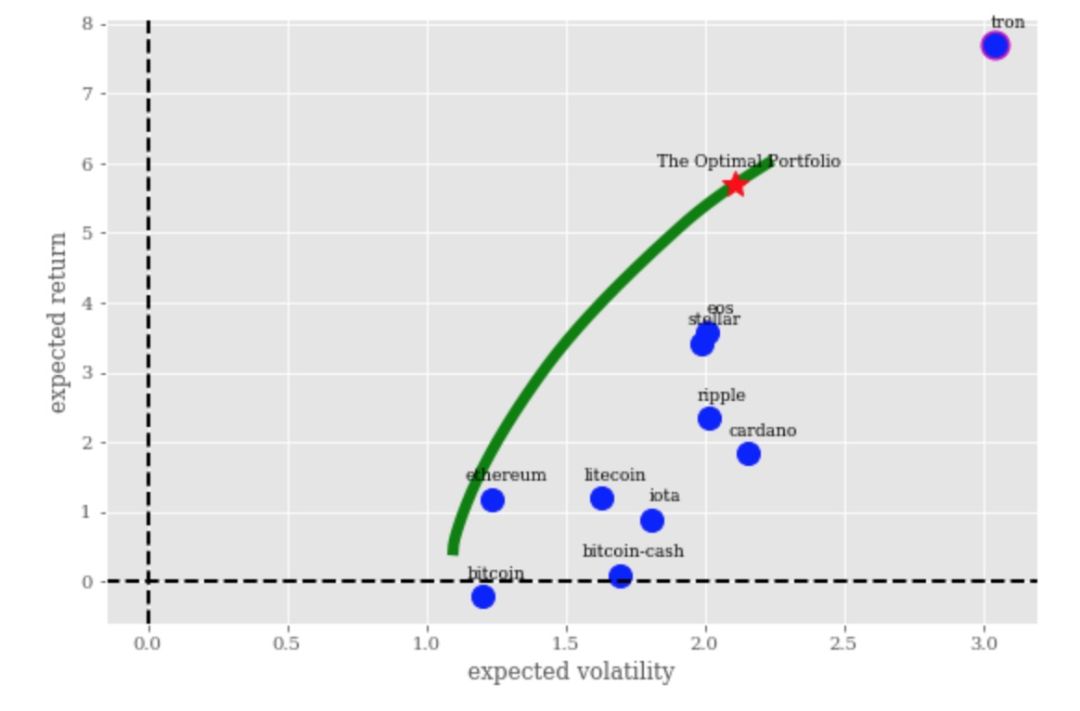
將有效邊界,最優投資組合和其它單一幣種的期望收益,標準差繪制在一張圖上,以對比風險分散的效果。從圖中可以看到,可以通過建立投資組合的方式提高夏普比率,提高投資效率。
5、結論
通過上面的測試,我們可以看到,投資組合理論的應用可以減少投資的相關性,分散非系統風險,并改善投資效果。關于傳統金融理論在數字貨幣投資中的應用,可供選擇和學習的模型還有很多,值得探究的領域也是俯拾即是。本文只是將傳統金融領域的經典模型應用到數字貨幣上的簡單探索,以后還會對更復雜的理論模型進行探索,謝謝大家的閱讀。
參考文獻:
【1】Zvi Bodie, Investments 10th edition
【2】Jonathan Berk, Peter DeMarzo, Corporate Finance 3th edition
【3】Harry Markowitz, Portfolio Selection
【4】Wes McKinney, Python for Data Analysis
本報告由火幣區塊鏈研究院出品,作者:袁煜明,彭俊豪,杜海
